计数与概率
集合
集合是数学中的一个基本概念,通俗地理解,集合是由一些不重复的数据组成的。比如 { 1 , 2 , 3 } \{1,2,3\} { 1 , 2 , 3 } 1 , 2 , 3 1,2,3 1 , 2 , 3
集合的特性
给定一个集合,任给一个元素,该元素或者属于或者不属于该集合,二者必居其一,不允许有模棱两可的情况出现。
一个集合中,任何两个元素都认为是不相同的,即每个元素只能出现一次。
一个集合中,每个元素的地位都是相同的,元素之间是无序的。集合上可以定义序关系,定义了序关系后,元素之间就可以按照序关系排序。但就集合本身的特性而言,元素之间没有必然的序。
集合和元素的关系
只有 a ∈ S a \in S a ∈ S a ∉ S a \notin S a ∈ / S
集合和集合的关系
子集与真子集
设 S , T S,T S , T S S S T T T S S S T T T S ⊆ T S⊆T S ⊆ T S , T S,T S , T S S S T T T S S S T T T S ⊂ T S⊂T S ⊂ T
集合的其他概念
有一类特殊的集合,它不包含任何元素,称之为空集,记为 ∅ \emptyset ∅
在一个相对固定的范围内所有元素的集合叫做全集。比如在立体几何中,全集是由空间的全体点组成的集合。
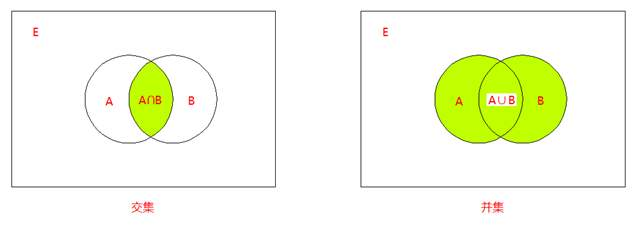
交集定义:由既属于 A A A B B B A ∩ B A \cap B A ∩ B
并集定义:由所有属于集合 A A A B B B A ∪ B A \cup B A ∪ B
差集定义:设 S S S A A A S S S S S S A A A A A A S S S S − A S-A S − A
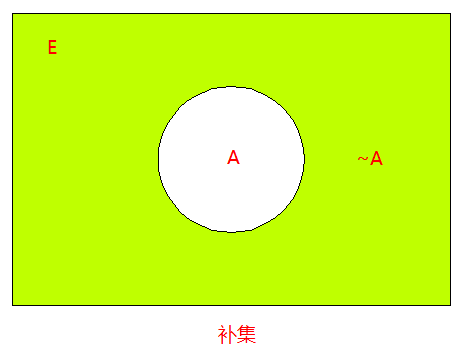
补集定义:设 E E E E − A E-A E − A A A A ∼ A ∼A ∼ A
计数基本原理
加法原理
假定 x 1 , x 2 , x 3 , ⋯ , x t x_1,x_2,x_3,⋯ ,x_t x 1 , x 2 , x 3 , ⋯ , x t i i i n i n_i n i { x 1 , x 2 , ⋯ , x t } \{x_1,x_2,⋯ ,x_t\} { x 1 , x 2 , ⋯ , x t } 两两不相交的集合 ,则可以从 x 1 , x 2 , x 3 , ⋯ , x t x_1,x_2,x_3,⋯ ,x_t x 1 , x 2 , x 3 , ⋯ , x t
n 1 + n 2 + ⋯ + n t n_1+n_2+⋯+n_t n 1 + n 2 + ⋯ + n t
乘法原理
如果一些工作需要 t t t n 1 n_1 n 1 n 2 n_2 n 2 t t t n t n_t n t 每一步选择独立 ),那么总的选择方案数为
n 1 × n 2 × ⋯ × n t n1×n2×⋯×nt n 1 × n 2 × ⋯ × n t
排列数
设 S S S n n n S S S r r r S S S r r r
S S S r r r A n r A_n^r A n r n = r n=r n = r A n r A_n^r A n r n n n r r r
从 n n n r r r 1 1 1 n n n 2 2 2 n − 1 n-1 n − 1 A n r A_n^r A n r
A n r = n ( n − 1 ) ( n − 2 ) . . . ( n − r + 1 ) A_n^r=n(n-1)(n-2)...(n-r+1) A n r = n ( n − 1 ) ( n − 2 ) ... ( n − r + 1 )
如果 n n n r r r 0 ≤ r ≤ n 0 \le r \le n 0 ≤ r ≤ n
A n r = n ! ( n − r ) ! A_n^r=\dfrac{n!}{(n-r)!} A n r = ( n − r )! n !
若 r > n r > n r > n A n r = 0 A_n^r = 0 A n r = 0
组合数
设 S S S n n n S S S r r r S S S r r r
S S S r r r C n r C_n^r C n r n n n r r r ( n r ) \tbinom{n}{r} ( r n )
如果 n n n r r r 0 ≤ r ≤ n 0≤r≤n 0 ≤ r ≤ n
C n r = n ! r ! ( n − r ) ! C_n^r = \frac{n!}{r!(n-r)!} C n r = r ! ( n − r )! n !
若 r > n r > n r > n C n r = 0 C_n^r = 0 C n r = 0
帕斯卡恒等式
是组合数中非常重要的公式:
C n k = C n − 1 k − 1 + C n − 1 k C_n^k=C_{n-1}^{k-1}+C_{n-1}^k C n k = C n − 1 k − 1 + C n − 1 k
可以用组合分析的方法证明:
从 n n n k k k C n k C_n^k C n k n − 1 n-1 n − 1 k − 1 k-1 k − 1 n − 1 n-1 n − 1 k k k C n − 1 k − 1 + C n − 1 k C_{n-1}^{k-1}+C_{n-1}^k C n − 1 k − 1 + C n − 1 k
鸽巢原理
鸽巢原理
又称为抽屉原理。其最简单的形式如下:
如果 n + 1 n+1 n + 1 n n n
Ramsey 定理
在 6 6 6 3 3 3
二项式定理
二项式系数
二项式系数其实就是一个组合数,可以用 C n k C_n^k C n k ( n k ) \tbinom{n}{k} ( k n ) n n n k k k
帕斯卡三角形
也叫杨辉三角,形式如下图。
第 n n n k k k C n k C_n^k C n k
二项式定理
设 n n n x x x y y y
( x + y ) n = ∑ k = 0 n C n k x k y n − k (x + y)^n = \sum\limits_{k = 0} ^ n C_n^k x^k y^{n-k} ( x + y ) n = k = 0 ∑ n C n k x k y n − k
其实就是两个数和 n n n
在二项式定理中,令 y = 1 y=1 y = 1
( x + 1 ) n = ∑ k = 0 n C n k x k (x + 1)^n = \sum\limits_{k = 0}^n C_n^k x^k ( x + 1 ) n = k = 0 ∑ n C n k x k
令 x = y = 1 x=y=1 x = y = 1
2 n = ∑ k = 0 n C n k 2^n = \sum\limits_{k = 0}^n C_n^k 2 n = k = 0 ∑ n C n k
令 x = 1 , y = − 1 x=1,y=-1 x = 1 , y = − 1
0 = ∑ k = 0 n ( − 1 ) k C n k 0 = \sum\limits_{k = 0}^n (-1)^k C_n^k 0 = k = 0 ∑ n ( − 1 ) k C n k
把上式移项,可以得到:
C n 0 + C n 2 + . . . = C n 1 + C n 3 + . . . = 2 n − 1 C_n^0 + C_n^2 + ... = C_n^1 + C_n^3 + ... = 2^{n - 1} C n 0 + C n 2 + ... = C n 1 + C n 3 + ... = 2 n − 1
也就是说,一个包含 n n n 2 n − 1 2^{n-1} 2 n − 1
可以这么想:对每个元素有 2 2 2 2 n 2^n 2 n n − 1 n-1 n − 1 n n n 2 n − 1 2^{n-1} 2 n − 1
计算组合数
如何计算一个组合数?最直观的方案是用组合数的公式:
参考代码如下: ‘ ‘ ‘ c p p i n t c o m ( i n t n , i n t m ) i n t r e s = 1 ; f o r ( i n t i = n ; i > = n − m + 1 ; i − − ) r e s = r e s ∗ i ; f o r ( i n t i = 1 ; i < = m ; i + + ) r e s = r e s / i ; r e t u r n r e s ; ‘ ‘ ‘ 这样计算的弊端是一来数据会很大,二来每计算一次复杂度很比较高,比较麻烦,三来对于一般的题目会对它有一个取模的要求,而除法其实是不太好取模的。我们在程序中预处理组合数一般利用帕斯卡恒等式。
参考代码如下:
```cpp
int com(int n, int m) {
int res = 1;
for (int i = n; i >= n - m + 1; i--) {
res = res * i;
}
for (int i = 1; i <= m; i++) {
res = res / i;
}
return res;
}
```
这样计算的弊端是一来数据会很大,二来每计算一次复杂度很比较高,比较麻烦,三来对于一般的题目会对它有一个取模的要求,而除法其实是不太好取模的。
我们在程序中预处理组合数一般利用帕斯卡恒等式。
参考代码如下: ‘‘‘ c pp in t co m ( in t n , in t m ) in t res = 1 ; f or ( in t i = n ; i >= n − m + 1 ; i − − ) res = res ∗ i ; f or ( in t i = 1 ; i <= m ; i + + ) res = res / i ; re t u r n res ; ‘‘‘ 这样计算的弊端是一来数据会很大,二来每计算一次复杂度很比较高,比较麻烦,三来对于一般的题目会对它有一个取模的要求,而除法其实是不太好取模的。我们在程序中预处理组合数一般利用帕斯卡恒等式。 参考代码如下:
const int mod = 1 e 9 + 7 ; int c[ 1005 ][ 1005 ]; void init ( int n , int m ) { for ( int i = 0 ; i <= n; i ++ ) { c[i][ 0 ] = 1 ; for ( int j = 1 ; j <= i && j <= m; j ++ ) { c[i][j] = (c[i - 1 ][j] + c[i - 1 ][j - 1 ]) % mod; } } } 这样,我们在 O ( n m ) O(nm) O ( nm ) C x y C_x^y C x y x ∈ [ 0 , n ] , y ∈ [ 0 , m ] x \in [0,n],y \in [0,m] x ∈ [ 0 , n ] , y ∈ [ 0 , m ]
概率初步
离散型随机变量
在概率论中,我们把一个随机实验的某种可能结果称为一个样本 ,把所有可能结果构成的集合称为样本空间 。在一个给定的样本空间中,我们把若干个样本构成的集合,即样本空间的子集,称为随机事件 。
我们把将样本映射为实数的函数称为随机变量 。当随机变量的取值有限或可数时,我们称该随机变量为离散型随机变量 ,反之当随机变量的取值不可数时,我们称该随机变量为连续型随机变量 。
在信息学竞赛中,我们主要需要讨论的是离散型随机变量。
概率的定义
设样本空间为 Ω Ω Ω Ω Ω Ω A A A P ( A ) P(A) P ( A )
(1) P ( A ) ≥ 0 P(A) \ge 0 P ( A ) ≥ 0
(2) P ( Ω ) = 1 P(Ω) = 1 P ( Ω ) = 1
(3) 对于若干个两两互斥事件 A i A_i A i ∑ P ( A i ) = P ( ∪ A i ) \sum P(A_i) = P(\cup A_i) ∑ P ( A i ) = P ( ∪ A i ) ∪ \cup ∪
则称 P ( A ) P(A) P ( A ) A A A 0 → 1 0→1 0 → 1