树状数组

引入

lowbit的求解

$lowbit(x) = x \& (-x)$

介绍

给定包含 $n$ 个数的数组 $a_1$ $a_2$ $a_3$ $...$ $a_n$。有两种操作:

查询区间 $[l,r]$ 数的和。把 $a_x$ 增加 $x$。

分析

与线段树的区别与联系

我们知道线段树的区间是按照中间点划分的，而树状数组是根据 $lowbit$ 来划分区间的。线段树的一个结点的区间是通过递归参数计算的，而树状数组的一个结点表示的区间可以根据结点标号计算出来，对于结点 $i$，其表示的区间为 $[i − lowbit(i) + 1, i]$，然后我们再用一个数组 $C$ 表示每个结点对应的区间内的数的和。 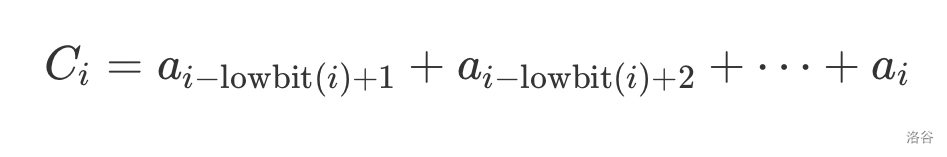下图为15个节点的树状数组： 灰色的结点是树状数组中的结点，每一层结点的 $lowbit$ 相同。而每个灰色结点 $i$ 和其后面的白色长条就代表了结点 $i$ 表示的区间。

查询

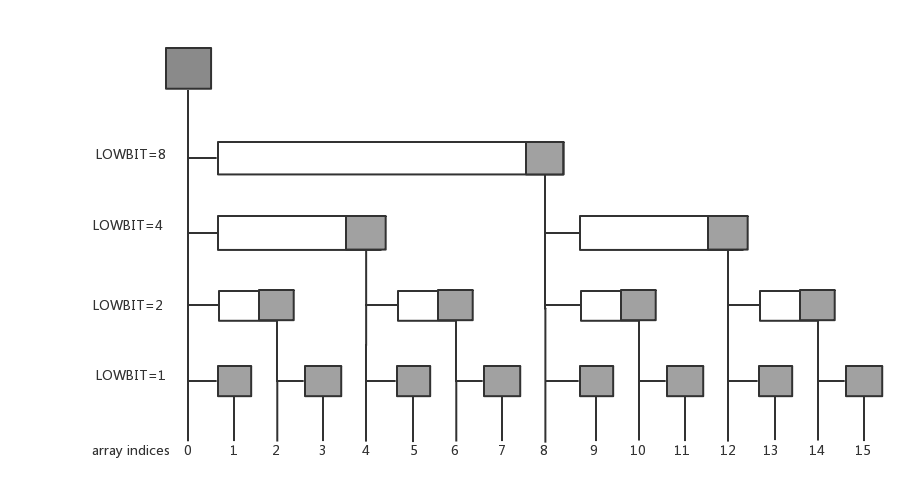
若要查询区间 $[l,r]$ 的和值，我们可以先求出 $[1,r]$ 的和值，然后减去 $[1, l − 1]$ 的和值。现在问题就是怎么求 $[1,x]$ 上的和值。实际上很简单

令 $sum=0$。

加上区间 $[x−lowbit(x)+1,x]$ 的和值。

然后令 $x=x−lowbit(x)$。

如果 $x=0$ 则退出，否则重复步骤 $1$。

$x=x−lowbit(x)$ 等价于将 $x$ 的二进制的最后一个 $1$ 减去。而 $x$ 的二进制里最多有 $\log x$ 个 $1$，所以查询效率是 $\log x$ 的。

例如查询 $[1, 11]$ 的和。

$sum = C[11] + C[10] + C[8]$

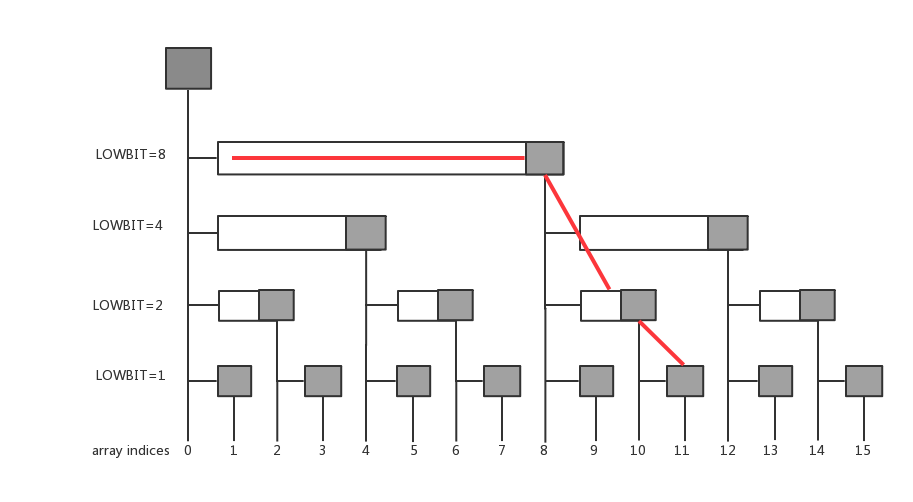
代码为：

int getsum(int x) {
    int res = 0;
    for (int i = x; i > 0; i -= lowbit(i)) {
        res += C[i];
    }
    return res;
}

更新

如果让 $a_x$ 增加 $v$，那么只有对于包含位置 $x$ 的区间的和值才会受到影响。而求出哪些区间受影响有一个巧妙的操作，就是一直令 $x=x+lowbit(x)$，直到 $x>n$，这一过程中所有的 $x$ 都是受影响的点。

如下图对应更新点 $3$。

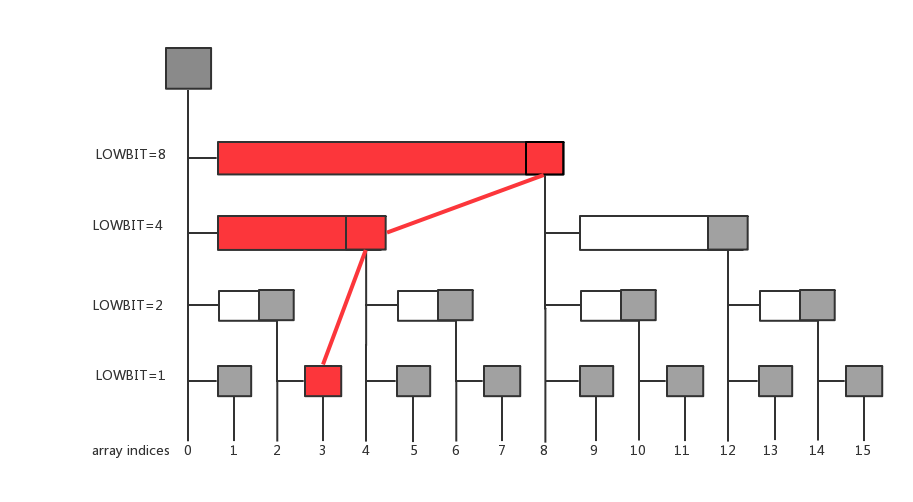
void update(int x, int v) {
     for (int i = x; i <= n; i += lowbit(i)) {
         C[i] += v;
    }
}

这一步的复杂度也是 $O(\log n)$。

性质

为什么树状数组只用来求区间和值？

因为树状数组只能求出区间 $[1,x]$ 的信息，用来求区间和只是通过前缀和转换了一下，所以如果是求区间最大（最小）值，就只能求区间 $1$ 到 $x$ 了，因为最大（最小）不满足加减的性质。

树状数组的比较方便，代码量小，并且常数较小。

数组数组能解决的问题是线段树的子集，线段树能解决树状数组不能解决的问题。

树状数组为什么没有建树，因为初始的时候，依次更新 $n$ 个元素代替了建树。当然线段树也可以这么做。